µZ: Series impedance vs input impedance

September 05, 2025

Introduction

When doing acoustic measurements with the µZ system, people often get confused by the abundance of words with 'impedance' in them. Each one has a different meaning. But what are these and what do they mean? When postprocessing a measurement, we have the choice from either series impedance or input impedance:

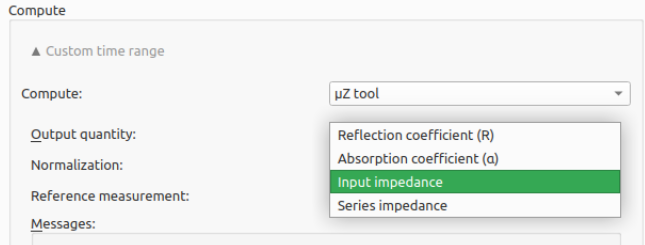
Screenshot of ACME, showing the µZ tool postprocessing output options

Here we are going to explain the details about these impedances.

µZ 4 microphone measurement method

When performing a measurement using the µZ system, a typical configuration is schematically shown below:

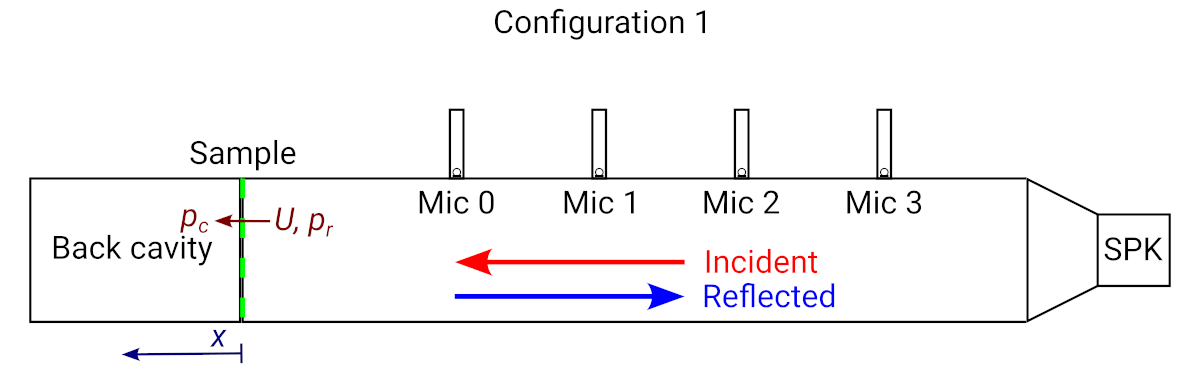
Impedance tube configured with a sample and back cavity

In this figure, the acoustic pressure ¹ at the tube side of the sample, is denoted by $p_r$. Note that the coordinate system $x$ has its origin at the sample, and is positive in the direction away from the speaker. The volume flow through the sample is defined as $U$. It is positive in the $x$-direction. The pressure at the sample, on the cavity side but directly at the location of the sample is $p_c$.

The red arrow indicates the incident wave and the blue arrow indicate the reflected wave. The incident and reflected wave can be measured using the microphones in the tube (on the right side of the sample). From these, the input impedance at the sample can be determined.

• The input impedance is the acoustic impedance at the sample as felt by the air in front of the sample, so it is defined as $Z_i =p_r/U$.
• The series impedance of the sample is defined as $Z_s = \left(p_r-p_c\right)/U$.

The acoustic properties of a sample can be defined by its series impedance if the sample is small with respect to the wavelength. In that case the volume flow $U$ is the same on both sides of the sample. This series impedance is a property of the sample², not of the system.

The input impedance is not only dependent on the sample, but also on what is on the other side of the sample. In the figure above this is a back cavity with a certain dimension.

Another possibility is an open end configuration:

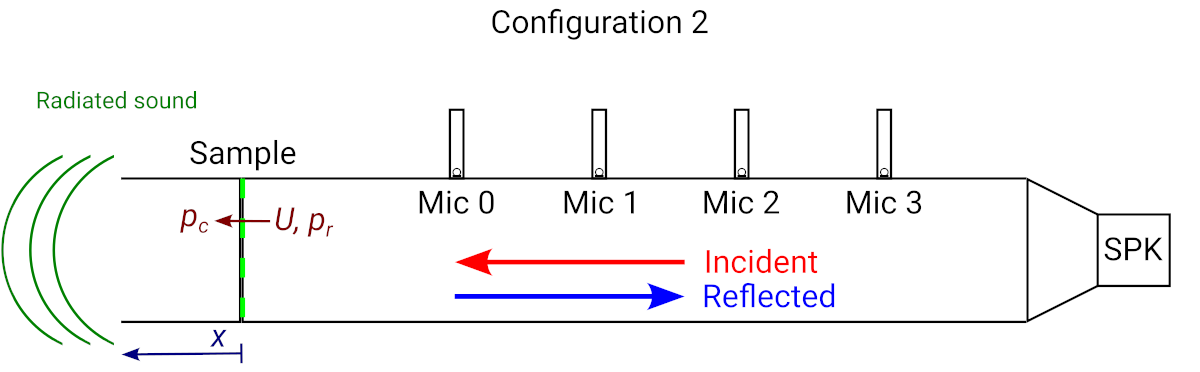
Impedance tube configured with a duct with open end behind the sample.

The behavior of the system in configuration 2 is significantly different from that in configuration 1. For example at low frequencies, it will become much harder to generate a high acoustic pressure on the open end side ($p_c$) of the sample, as all air pressure will leak away through sound radiation.

Why is input impedance important?

This is important for determining the right measurement method and getting a high accuracy. We will explain further.

Suppose the sample has a very low series impedance. In that case the input impedance will be completely determined by the boundary condition behind the system (open end vs closed end or others). The low frequency limit can typically be used to indicate what is happening:

• Configuration 1 gives an input impedance that grows indefinitely when we decrease the frequency to 0.
• Configuration 2 gives an input impedance of 0 when we decrease the frequency to 0.

The way we measure the sample series impedance is by computing the input impedance in two configurations. We keep the boundary condition on the left side of the sample the same. First we perform a reference measurement, where the input impedance is measured without sample. Then we perform the measurement with sample. By determining the input impedance again, the series impedance can be determined by subtracting the input impedance with sample from the case without sample.

This procedure only gives sensible results, when the two impedances differ significantly. Otherwise we are just measuring noise. Thus, the accuracy with which we can determine the series impedance of the sample depends on the accuracy with which we can measure the input impedance.

Impedance tubes have limitations on this, as it is typically difficult to accurately measure high standing wave ratios, due to the small phase differences that it introduces. In the configurations shown above, it is only possible to measure input impedance up to 10 to 50 times the magnitude of the characteristic acoustic impedance in the tube. Here, the characteristic acoustic impedance is the local pressure divided by the local volume flow for a plane propagating wave. If the series impedance of the sample is higher than that, the sample becomes indistinguishable from a "hard wall". This happens for small samples w.r.t. to the tube diameter, often combined with a high series impedance.

µZ 5 microphone measurement method

In case the input impedance can't be measured accurately using the default measurement method as described previously, the following configuration can be used:

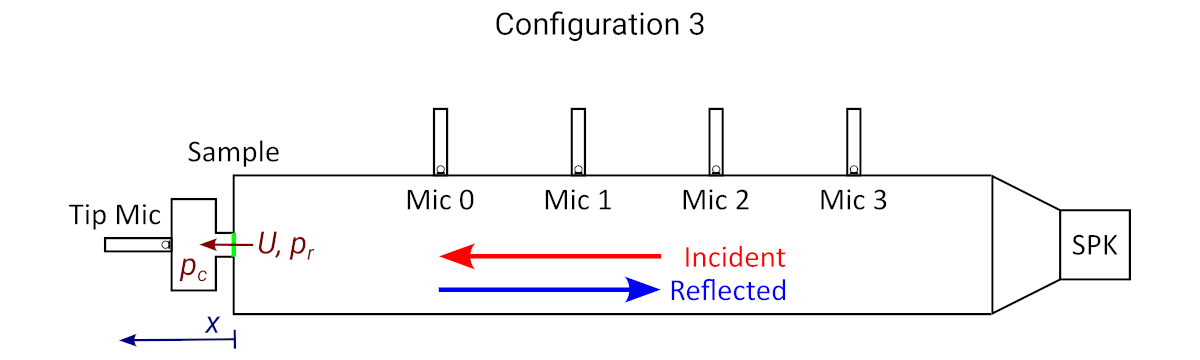
Impedance tube configured with a duct with open end behind the sample.

This configuration contains a 5^th microphone in a closed cavity behind the sample, which we call the tip microphone. The tip microphone captures the acoustic signal on the other side of the sample, which we call the tip microphone. Using the tip microphone, the volume flow through the sample can be obtained. For example for low frequencies, we know that the tip microphone signal is proportional to the $U/(i\omega)$, i.e. the amount of air that is displaced through the sample. As the tip microphone does not directly pick up the pressure behind the sample, a model is required to infer the $p_c$ from the tip microphone pressure.

At ASCEE, we have done careful analysis on the size of such a cavity. If we make the cavity too small this results in:

• Hardly any volume flow through the sample, resulting in the problem that we need to calculate the difference between two large numbers.
• Uncertainties due to viscothermal losses in the cavity. For example the compression / expansion will become more isothermal, instead of adiabatic.

On the other hand, if we make the cavity too large this results in:

• A too small signal at the tip microphone, resulting in noisy measurements.
• At high frequencies, we will have wave effects in the cavity, that require a more complicated cavity model. This is accompanied by extra uncertainty.

All in all, we conclude that the cavity size needs to be chosen carefully, taking all aspects of the measurement system into account. Including the sample to be measured.

Takeaways

• Series impedance is a material property
• Input impedance is a property of both the sample and the configuration behind the sample. It is important for determining the measurement range and system configuration

In my next post, we will dive into the different normalization options that are in use. Learn more on determining the right measurement configuration for µZ measurements.